Math is not Science / Was Euler Wrong?

[BigBoss]

you guys are fucking nerds


go outside and hang out with some girls, for the love of god....

[GenePeer]

Square-root of a number, z, means a number if multiplied by itself gives z. Other than convention, there's no reason why square-root of 1 must be 1 and not -1.

Since it seems people only believe me when I post outside links: http://mathworld.wolfram.com/SquareRoot.html
http://mathworld.wolfram.com/PrincipalSquareRoot.html

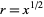If you read those links, you'll realize that sqrt(x) or means the principal square-root. But never once did that statement by Euler mention "principal square-root", so your translation to math is false. It should be:
±sqrt(-1*-1)=±sqrt(-1)*±sqrt(-1)

which is true.

[GenePeer]

If my teacher asked what the square-root of 4 is, and I said -2, I wouldn't be wrong. Even though, it's not the answer (s)he might be expecting, I'd still be right.

Simply saying Euler was wrong because what he said doesn't conform with the conventions is ridiculous. You know what a definition of a square-root is (the one I gave) but somehow you're convinced Euler wasn't using this definition. Why? Unless he specifically wrote sqrt(a*a) = sqrt(a)*sqrt(a), you can't claim he was wrong. PROBABLY that's what he meant, therefore he was PROBABLY wrong.

Seriously though, I know even geniuses can make mistakes, but your example wasn't one of them.

This thread is turning into academic waffle from both sides. lol. If you want to have actual discussions about concepts in math and not the meaning of notation, then I'm down.

When I created this thread, I wanted to show people that Math is not a science. I have no idea whether I've achieved my goal or how I can be more articulate/elaborate/whatever. If you still think math is science, then to each their own.

[BigBoss]

i know its hard but eventually you guys gotta come out your rooms

[Alex2012]

I think what I understood that the mathematician asserts and the scientist confirms.

or the opposite

[GenePeer]

Well put, but I'm claiming the opposite.

[Alex2012]

Well put, but I'm claiming the opposite.

Why?























































I joke.

but I'll still think about it!

[GenePeer]

If my teacher asked what the square-root of 4 is, and I said -2, I wouldn't be wrong. Even though, it's not the answer (s)he might be expecting, I'd still be right.

If your teacher asked what a square root of 4 is (so she/he is implying the existence of more than one with their language), and you replied -2...you wouldn't be wrong. If your teacher asked you what THE square root of 4 is (implying that there is only one), and you replied -2, you would be wrong. "THE" implies "principal."

This is purely conventional. There is no law in math where THE means principal.

I'm sorry but you've got it all wrong. It's the other way round. It's not interesting at all to refer to a square (or n-th) root of a number as just one number. All these numbers share the same property and favoring one over the other because it's 'positive' is really not mathematically interesting. So when you're finding "the" sixth-root of i, which one will you favour and why? Please answer this.

When someone talks about the cube root of 1, nobody is ever referring to the number -1/2 + sqrt(3)*i/2. Lmao. They're referring to the number 1.

I don't know about you, but this was actually very important in my last year when I studied complex numbers. Whenever an n-th root was asked for, I HAD to list all n roots.

Unless he specifically wrote sqrt(a*a) = sqrt(a)*sqrt(a), you can't claim he was wrong.

Um, he DID write that, except he used two different numbers, not the same number.

I'm going to take your word on this. Fine he was wrong...

PS: "the square root of 4" and "sqrt(4)" are two different things. The later is specifically defined as the principal square-root. The former would thus be "±sqrt(4)".

[GenePeer]

I remember diction once telling you something like every argument you're in ends up being about grammar. I can't believe it's happening to my math thread. If the reason I'm wrong is because (s)he said "the" instead of "a", then the problem is effectively a trick question testing my understanding of English.

Seriously, why are you being such a prick over tiny little details that are easily understood among mathematicians? When someone says "the square-root of 4", it has an ambiguous meaning. If it's interpreted as "principal square-root" and things become false (like in Euler's case) but when interpreted as "A square-root" and things make sense, then you get over it and understand that's what he meant for fuck's sake. Until he explicitly shows what he meant through formulae (sqrt(a*a)=sqrt(a)*sqrt(a) vs. ±sqrt(a*a)=±sqrt(a)*±sqrt(a)), you're just being a dick correcting him. Euler didn't even speak English, what makes you so sure it's not the translator's fault for writing "the" instead of "a".

And here is the case when x is not positive or zero, therefore it's not clear which root is being referred to.

An that's why it's not interesting to make anything special. Here you have a term that can be used by all sorts of number (negative, complex) or matrices and what-not, but for some reason, is treated to mean something different/special when applied to positive real-numbers.

In common usage, unless otherwise specified, "the" square root is generally taken to mean the principal square root.

Wait, now "generally" means "all the time to you"?

They are exactly the same thing. "sqrt(4)" is the mathematical translation of the English term "the square root of 4," and vice versa. Both mean principal.

Any nonnegative real number x has a unique nonnegative square root r ; this is called the principal square root and is written or .

I'm telling (showing) you the definition of "sqrt(4)" is "the principal square-root of 4", but you're just ignoring it. As far as this discussion goes, you're wasting my time.

Edit:
That wasn't just my teacher telling me to list everything, it's the International Baccalaureate aka IB. They've been administering exams for decades and all of a sudden, YOU think they don't qualify. Give me a break.

[GenePeer]

Ok then, 98% of mathematicians will not agree with "the square-root of 4 is not -2".

You asked me what the sixth root of an imaginary number is, when I was clearly talking about the principal square root function, which takes non-negative REAL numbers only.

You claim Euler said sqrt(a*a)=sqrt(a)*sqrt(a), and to prove him wrong you said sqrt(-1*-1)=sqrt(-1)*sqrt(-1) is false. Hold on, I thought you just said principal square root function takes in non-negative REAL numbers, so why are you doing sqrt(-1)? Clearly, if he meant the principal square root then you can't prove him wrong by passing invalid arguments to the function.

[GenePeer]

If you're going to extend the square-root to be used on -1, then the n-th root can also be used on -1. And when it's high, like 10-th root, you can no longer choose which one root to take. So if it eventually breaks, why use it in the first place?

When I'm asked for the square-root of 4, I say "the square-root of 4 is 2 or -2." There's is nothing wrong with this.

I've just stopped taking your word for it now. Can you provide a link of where he gave that specific equation? If all he ever said was your first quote, then there's reason to believe he meant

±sqrt(A) * ±sqrt(B) = ±sqrt(A*B) for all real numbers

[GenePeer]

What did Euler actually claim about the multiplication of radicals? The answer is not straightforward, because nowhere in the Algebra did he even write the equations sqrt(a)*sqrt(b) = sqrt(ab)...

Surprise

Also, his expression “the square-root of a given number always has a double value” suggests that his frequent use of the singular phrase “the square-root” did not mean that only single solutions are obtained

That's what I've been trying to argue the whole time.

In the end, it comes down to a choice of axioms. If we assume that all square roots have two values and require the fourfold multiplication of double signs, then Euler’s results are justifiable. Otherwise, the product rule can be restricted by positing independent rules like (5), (6), or (7).

Conventions, conventions... this argument isn't going anywhere. I give up.

LOL.

"Euler defined mathematics as the science of quantity, where “quantity” signifies that
which can be increased or decreased."

Even Euler thought math is a science.

The scientific model/method was only recently formulated, so the science he's talking about isn't necessarily the same we're talking about...

Can we agree to disagree? I just want to move on now.

[GenePeer]

I am tempted to respond to that, but I will be doing nothing but fueling more countless pages of essentially the same thing.

It was nice having this debate, and honestly, I have more respect for you than EmBase who only resorted to insulting me in the other thread.

[iain08]

I enjoyed this.